Método de dibujo para ampliar y reducir imágenes
LUIS ALBERTO ROMERO HERNÁNDEZ
© Método de dibujo para ampliar y reducir imágenes
© Texto de la idea original del autor inscrito en el Registro General de la Propiedad Intelectual, del Ministerio de Cultura del Gobierno de España, con Número de Asiento Registral 00/2019/2658, con fecha 15 de marzo de 2019.
© Artículo publicado con DOI 10.20868/ardin.2021.10.4526 en el número 10 de la revista digital ARDIN (Arte, Diseño e Ingeniería) de la Universidad Politécnica de Madrid, el 26 de marzo de 2021.
© Autor de los textos: Luis Alberto Romero Hernández
© Autor de las ilustraciones: Luis Alberto Romero Hernández
Prólogo
Para ampliar o reducir una imagen dada, los métodos utilizados hasta la fecha estaban basados en la homotecia, en el uso práctico de la teoría de la pirámide visual, en operaciones matemáticas a través de la proporción y de una constante numérica, en cuadrículas, en utensilios mecánicos de muy diversa índole o en sistemas fotográficos, de proyección, electrónicos o digitales. El presente estudio desarrolla paso a paso, de manera didáctica y detallada, un nuevo método de ampliación y reducción de cualquier tipo de imágenes, de cualquier forma, de cualquier tamaño, de cualquier formato, en cualquier orientación, en un retorno a lo artesanal frente a los actuales sistemas tecnológicos, sin la necesidad de utilizar números, con el uso exclusivo de simples útiles de dibujo, basado únicamente en la geometría, a través de la proporción y la semejanza de triángulos. Este método puede tener aplicaciones a nivel global, no solo en la pintura de caballete y en el dibujo de estudio, sino también en la pintura mural y el grafiti, y en otros ámbitos que pueden ir desde la jardinería hasta la ingeniería.
1. Introducción.
Una de las principales dificultades con las que se encuentran los artistas profesionales y los aficionados a la hora de dibujar es el hecho de tener que copiar una imagen, ya sea esta un dibujo, una pintura o una fotografía, en otro formato distinto al de dicha imagen dada, formato que habitualmente suele ser mayor que ella (Ulrich, 1974). Para ello, hay que mantener de manera escrupulosa una correlación entre el original y la ampliación, basada en la razón de semejanza y en la semejanza, términos propios del ámbito de la geometría y de las matemáticas. La razón de semejanza es la constante de proporcionalidad entre los lados de figuras semejantes, y corresponde al número por el que hay que multiplicar las longitudes de los lados de una de las figuras para obtener las longitudes de los lados de la otra. La proporcionalidad es la relación de correspondencia que guardan dos magnitudes. La semejanza es la operación geométrica que transforma una figura en otra figura semejante. Así pues, la semejanza transforma una figura en otra que tiene los mismos ángulos, y los lados proporcionales.
Euclides (1994) recoge esas ideas en sus Elementos (Libros 5º-9º), según se menciona en las definiciones de su libro 5º: “Una razón es determinada relación con respecto a su tamaño entre dos magnitudes homogéneas” (p. 9), “Llámense proporcionales las magnitudes que guardan la misma razón” (p. 12), y de su libro 6º: “Figuras rectilíneas semejantes son las que tienen los ángulos iguales uno a uno y proporcionales los lados que comprenden los ángulos iguales” (p.55).
Cabe recordar que la premisa básica para copiar una imagen en un soporte de distinto tamaño es que ambos formatos han de ser proporcionales (CEAC Ed., 2002). Para ello es sabido que, haciendo coincidir una esquina de la imagen con su correspondiente (homóloga) del soporte, de modo que coincidan los lados, trazando una diagonal desde dicha esquina hasta la esquina opuesta de la imagen y proyectando dicha diagonal sobre el soporte, esta diagonal ha de coincidir también con la esquina opuesta del soporte. Esto está basado en la definición de triángulos semejantes (dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales), y en el Teorema primero de Tales de Mileto:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.
Hasta ahora, por lo que se conoce en academias de arte, en manuales de dibujo de distintas épocas de la historia, en el trabajo cotidiano de los artistas actuales y en la carrera de Grado Universitario en Bellas Artes, los sistemas de cambios de escalas (las ampliaciones son las más frecuentes) se basaban en el uso de cuadrículas más elaboradas o más sencillas (Lawson, 1958), (Maveco Ed., 1987), (Ubach Ed., 2008), en la homotecia, en la multiplicación de las distintas medidas de la imagen dada por una razón constante, en la aplicación de la conocida “regla de tres”, en la puesta en práctica puntual del Teorema de Tales para hallar ciertos segmentos proporcionales, o en la utilización del compás de proporción o reducción, o del pantógrafo. Desde la llegada de las fotocopiadoras y demás impresoras, muchos artistas han agilizado el trámite de pasar una imagen a otro formato mayor por medio de las ampliaciones que esas máquinas permiten realizar de manera rápida y exacta, pasando posteriormente la ampliación al soporte por algún método de calcado. Igualmente cómodo es el uso de cualquier sistema de proyección a través de diferentes instrumentos eléctricos ópticos, como puede ser el proyector de opacos.
Existen fórmulas menos ortodoxas, más intuitivas, que seguramente muchos artistas utilicen en la intimidad de sus estudios, como interponer con una mano la imagen a copiar a la distancia apropiada entre un ojo (cerrando el otro) y el soporte, localizando por medio de la teoría de la pirámide o el cono visual el lugar de cada punto, que se va marcando con un lapicero o similar con la otra mano, mientras se quita y se pone intermitentemente la imagen. En este método caben varias posibilidades, como mantener la imagen “a pulso” o por el contrario situarla sobre algún tipo de mesa de cristal que permita poder colocar el soporte bajo ella, soporte en el que se dibujará mientras se mira a través del cristal de dicha mesa, poniendo y quitando intermitentemente la imagen. Otra variante de este método (que también puede realizarse “a pulso” o sobre mesa de cristal) es que la imagen, en lugar de ser opaca, sea algún tipo de acetato transparente con el dibujo realizado con tinta permanente como la de los rotuladores indelebles, lo cual permite la visualización del soporte a través de dicho acetato, haciendo más fácil el concepto de pirámide visual. Una variante más de este sistema, basada en el “método del vidrio” (Da Vinci, 2010), es la posibilidad de realizar una reducción, poniendo la imagen bajo el cristal de la mesa, a la distancia apropiada, y colocando sobre el cristal un acetato en el que se puede dibujar con tinta permanente -siempre cerrando un ojo-, la imagen dada, que después se podrá pasar a un soporte opaco con el método de copiado que se considere más apropiado. (La tinta permanente se elimina con alcohol, con lo cual pueden reutilizarse los acetatos). Todos estos métodos se mencionan aquí como fórmulas para copiar una imagen plana en otro soporte proporcional, pero durante muchos siglos se han inventado y utilizado diversos útiles para copiar escenas del natural (Barbero et al., 2002), como es el caso de la cuadrícula portátil (Szunyoghy, 2013).
Al margen de todos estos procedimientos, en el presente estudio se expone un nuevo método, diferente, que supone una solución práctica al problema técnico de cualquier tipo de copia a distinta escala manteniendo perfectamente la proporcionalidad, y que puede ser utilizado tanto en el ámbito artístico como en el técnico e industrial. Es cómodo y limpio, y con él no hay que utilizar números, ni hace falta escuadra, cartabón o semicírculo graduado.
El origen de este método surgió en el seno del proceso dibujístico del autor. Muchas de sus obras pictóricas parten de una fotografía inicial. Guiado por el interés en una escrupulosa exactitud en el dibujo, el autor casi siempre utiliza alguno de los métodos mencionados más arriba para copiar una imagen en otro formato. Al poner en contacto la fotografía inicial sobre el soporte con el dibujo ya finalizado, manteniendo siempre la misma orientación y el paralelismo entre ambos, se ponga donde se ponga la fotografía sobre el soporte, un único punto de la fotografía coincide con su punto correspondiente en el soporte (“punto de coincidencia”).
El núcleo del presente estudio se encuentra en la relación que existe entre ese “punto de coincidencia” y los formatos, proporcionales, de imagen y soporte. Cada “punto de coincidencia” es el resultado de la intersección de las rectas que parten de dicho punto hasta cada una de las esquinas de la imagen y que se prolongan hasta cada una de sus esquinas homólogas del soporte. Aprovechando esta idea, partiendo de una imagen dada y de un soporte mayor, proporcional, sobre el cual se quiere dibujar la ampliación, puede localizarse en dicho soporte el punto correspondiente a cada punto de la imagen dada, a través de la triangulación.
2. Triangulación.
Para trasladar un punto dado de una imagen a un soporte mayor hay que conocer qué relación tiene dicho punto con el formato de la imagen a la que pertenece. Con los métodos de ampliación conocidos hasta el momento, un punto de una imagen puede localizarse a través de coordenadas (cuadrícula), o bien por la distancia perpendicular a la que se encuentra de los lados de la imagen (alto y ancho), trasladando dichas medidas a través de una razón al soporte final. Según el método del presente estudio esa relación está basada en que un punto de una imagen puede triangularse con dos esquinas de dicha imagen. Para triangular un punto dado (localizar su posición exacta en un plano) hay que contar con otros dos puntos auxiliares conocidos y unir los tres puntos con rectas, formando un triángulo, siendo obviamente condición obligatoria que los tres puntos no pertenezcan a la misma recta. Los ángulos que forman en los dos puntos auxiliares los laterales del triángulo así construido, y la distancia conocida entre esos dos puntos auxiliares, confirmarán la posición exacta del punto dado. Ese principio de triangulación es la base del presente método de dibujo. Para desarrollar didácticamente este método lo más apropiado es partir de un formato rectangular, por ser el más habitual. Cada punto de una imagen puede triangularse a través de, al menos, dos esquinas de dicha imagen.
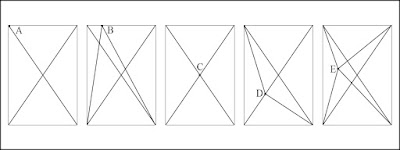
Si el punto dado A es una esquina, uniéndolo con una recta con la esquina opuesta (trazando la diagonal de la imagen), se consigue que dicho punto sea vértice de dos triángulos. Si se traza la otra diagonal de la imagen surge un triángulo más, que también tiene el punto dado como vértice, y dos esquinas de la imagen como los otros dos vértices.
Si el punto dado B se encuentra en un lateral (cualquier lado, entre dos esquinas), se puede unir dicho punto con las dos esquinas que no comparten tal lateral, a través de sendas rectas, consiguiendo que dicho punto sea vértice de tres triángulos. Si se trazan las dos diagonales de la imagen surgen dos triángulos más, que también tienen el punto dado como vértice, y dos esquinas de la imagen como los otros dos vértices.
Si el punto dado C está en el “interior” de la imagen, en su centro (en la intersección de sus dos diagonales), se puede unir dicho punto con las cuatro esquinas de la imagen, consiguiendo que dicho punto sea vértice de cuatro triángulos.
Si el punto dado D está en el “interior” de la imagen, en una diagonal, se puede unir igualmente dicho punto con las cuatro esquinas de la imagen, consiguiendo que dicho punto sea vértice de cuatro triángulos. Si se traza la diagonal en la que no está el punto dado surge un triángulo más, que también tiene el punto dado como vértice, y dos esquinas de la imagen como los otros dos vértices.
Si el punto dado E está en el “interior” de la imagen, sin ser el centro ni estar en una diagonal, se puede unir igualmente dicho punto con las cuatro esquinas de la imagen, convirtiendo la imagen en cuatro triángulos. Si se trazan las dos diagonales de la imagen surgen dos triángulos más, que también tienen el punto dado como vértice, y dos esquinas de la imagen como los otros dos vértices. (Fig. 1).
Figura 1. Triangulaciones.
La cuestión es relacionar un punto dado con otros dos puntos fijos conocidos de la imagen (dos esquinas), para obtener un triángulo, y poder trasladarlo al soporte. Para ello se cuenta con los dos datos que son condición necesaria y suficiente para obtener un triángulo en el soporte, semejante a uno de la imagen: un lado proporcional y dos ángulos iguales. El lado o la diagonal de la imagen que comparten los dos vértices escogidos, y su lado o su diagonal correspondientes del soporte son proporcionales. Por otra parte, los dos ángulos que parten de sendos vértices hacia el punto dado han de ser iguales en imagen y soporte. Para ello -y aquí se encuentra la piedra angular de este método-, basta hacer coincidir la imagen sobre el soporte en ambas esquinas seleccionadas y prolongar los ángulos. De este modo, el triángulo resultante en el soporte es semejante al de la imagen, así que el punto localizado en el soporte es el punto buscado, correspondiente al punto dado de la imagen.
Existen otros sistemas de triangulación, como los utilizados en topografía, basados en diversos métodos de medición de distancias y de ángulos, apoyados en distintas tecnologías y en el uso de fórmulas matemáticas, trigonométricas. Así, para la triangulación de terrenos se cuenta con los métodos de “Intersección directa”, “Intersección inversa”, “Radiación simple” o “Radiación doble”. El presente método se asemejaría a la “Intersección directa” y en menor medida a la “Radiación doble”. Dadas las dimensiones que han de tratarse en el ámbito topográfico, la utilización de instrumentos y de tecnología cada vez más avanzada se hace imprescindible, pero aunque las formulaciones matemáticas y los recursos técnicos utilizados en topografía sean mucho más complejos que el sistema descrito en el presente estudio, en ambos casos se comparte la premisa de triangular espacios para conocer y representar puntos, distancias y superficies.
3. Procedimiento de ampliación.
3.1. Genérico.
Así pues, partiendo de una imagen dada OPRQ y de un soporte proporcional a ella O’P’R’Q’ (la diagonal O’R’ es proporcional a la diagonal OR), se puede localizar en el soporte la posición exacta de cada punto de la imagen dada, a partir del concepto de triángulos semejantes entre imagen y soporte. Para ello basta con seguir los pasos que se describen a continuación.
(Como formato más generalizado, se parte del rectángulo. Con el formato cuadrado se actuaría de igual modo, y el resto de posibles formatos se tratarán más adelante). (Fig. 2).
Figura 2. Procedimiento de ampliación. Genérico.
3.1.1. Se localiza el punto A de la imagen.
3.1.2. Se hace coincidir la esquina O de la imagen sobre su esquina homóloga O’ del soporte, de manera que coincidan los lados de la imagen que parten de O con los lados correspondientes del soporte, que parten de O’. De ese modo, el punto de coincidencia entre imagen y soporte es la propia esquina, O=O’.
3.1.3. Se unen con una línea recta s mediante una regla los puntos O y A, y se prolonga dicha recta s sobre el soporte. Es pertinente aclarar aquí que siempre que se habla de emplear una regla se entiende que también se puede emplear cualquier otro método de prolongación, como un cordel, cuando las dimensiones del soporte final sean muy grandes.
3.1.4. Se hace coincidir la esquina P de la imagen sobre su esquina homóloga P’ del soporte, de manera que coincidan los lados de la imagen que parten de P con los lados correspondientes del soporte, que parten de P’. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, P=P’).
3.1.5. Se unen con una línea recta t mediante una regla los puntos P y A, y se prolonga dicha recta t sobre el soporte.
3.1.6. El punto de intersección en el soporte de las rectas s y t es el punto A’, que es la localización correspondiente exacta en el soporte del punto A de la imagen, que es lo que se buscaba.
Para este método basta con utilizar dos esquinas, pero si surgen dudas siempre podrá repetirse el proceso con una tercera esquina, e incluso con la cuarta.
3.2. Laterales de la imagen.
Si los puntos a trasladar se encuentran en alguno de los cuatro laterales de la imagen, el método descrito en los pasos 3.1.1. al 3.1.6. seguiría siendo completamente válido, pero al ser los lados de la imagen líneas básicas especiales, el método se simplifica, siguiendo estos pasos: (Fig. 3):
Figura 3. Procedimiento de ampliación. Laterales de la imagen.
3.2.1. Se localiza el punto B del lado OP.
(Para este procedimiento especial no podrá utilizarse como vértice de coincidencia ninguna de las dos esquinas que delimitan el lado en el que se encuentra el punto dado. En este caso, no podrá utilizarse ni la esquina O ni la esquina P, sino alguna de las otras dos esquinas, Q o R).
3.2.2. Se hace coincidir la esquina Q de la imagen sobre su esquina homóloga Q’ del soporte, de manera que coincidan los lados de la imagen que parten de Q con los lados correspondientes del soporte, que parten de Q’. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, Q=Q’).
3.2.3. Se unen con una línea recta u mediante una regla los puntos Q y B, y se prolonga dicha recta u sobre el soporte, hasta la intersección con el lado O’P’ del soporte.
3.2.4. El punto de intersección entre la recta u y el lado O’P’ será el punto B’, que es la localización correspondiente exacta en el soporte del punto B de la imagen, que es lo que se buscaba.
Se puede comprobar fácilmente que se obtendría exactamente el mismo punto B’ si se parte de la otra esquina, R, como vértice de coincidencia.
3.3. Diagonales de la imagen.
Hay que tener en cuenta que si el punto que se quiere trasladar se encuentra justo en una de las dos diagonales de la imagen, no podrán ser las dos esquinas unidas por esa diagonal las utilizadas para triangular dicho punto, lógicamente, pues según ya se ha comentado, es regla básica que tres puntos que están localizados en una misma recta no pueden formar un triángulo. En este caso podrán utilizarse las dos esquinas restantes, o una de estas dos esquinas restantes y una de las esquinas unidas por la diagonal sobre la que se encuentra el punto dado, y el método descrito en los pasos 3.1.1. al 3.1.6. seguiría siendo completamente válido, pero al ser las diagonales de la imagen líneas básicas especiales, el método se simplifica, siguiendo estos pasos: (Fig. 4):
Figura 4. Procedimiento de ampliación. Diagonales de la imagen.
3.3.1. Se localiza el punto C de la diagonal OR.
(Para este procedimiento especial no podrá utilizarse como vértice de coincidencia ninguna de las dos esquinas que delimitan la diagonal en la que se encuentra el punto dado. En este caso, no podrá utilizarse ni la esquina O ni la esquina R, sino alguna de las otras dos esquinas, P o Q).
3.3.2. Se hace coincidir una de las dos esquinas de la imagen que no sea vértice de la diagonal dada, P, sobre su esquina homóloga P’ del soporte, de manera que coincidan los lados de la imagen que parten de P con los lados correspondientes del soporte, que parten de P’. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, P=P’).
3.3.3. Se unen con una línea recta v mediante una regla los puntos P y C, y se prolonga dicha recta v sobre el soporte.
3.3.4. Se localiza con una regla sobre el soporte la diagonal O’R’.
3.3.5. El punto de intersección entre la recta v y la diagonal O’R’ será el punto C’, que es la localización correspondiente exacta en el soporte del punto C de la imagen, que es lo que se buscaba.
Se puede comprobar fácilmente que se obtendría exactamente el mismo punto C’ si se parte de la otra esquina, Q, como vértice de coincidencia.
Si se comprueba que el punto a trasladar se encuentra en la intersección de las dos diagonales de la imagen (el centro de la imagen), aunque para este supuesto el método descrito en los pasos 3.1.1. al 3.1.6. seguiría siendo completamente válido (mientras se utilicen dos vértices adyacentes), obviamente se optará simplemente por trazar las diagonales en el soporte para hallar el punto central buscado.
4. Variedad de formas.
4.1. Genéricas.
Si la figura de la imagen dada que se quiere trasladar al soporte es cualquier tipo de forma poligonal compuesta por líneas rectas, sólo se tendrá que localizar en el soporte cada uno de los vértices de dicha figura, para después unirlos con una regla mediante líneas rectas homólogas.
Si la línea de la imagen dada que se quiere trasladar al soporte es curva, se elegirán unos cuantos puntos para trasladarlos al soporte y después se completará la línea.
4.2. Circunferencia.
Si la línea que se quiere trasladar es una circunferencia se procederá siguiendo estos pasos: (Fig. 5):
Figura 5. Variedad de formas. Circunferencia.
4.2.1. Se localiza el punto central E de la circunferencia dada mediante el método de dibujo que se considere más apropiado.
4.2.2. Se hace coincidir la esquina O de la imagen sobre su esquina homóloga O’ del soporte, de manera que coincidan los lados de la imagen que parten de O con los lados correspondientes del soporte, que parten de O’. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, O=O’).
4.2.3. Se unen con una línea recta w mediante una regla los puntos O y E, y se prolonga dicha recta w sobre el soporte. La recta w corta a la circunferencia en el punto F.
4.2.4. Se hace coincidir la esquina P de la imagen sobre su esquina homóloga P’ del soporte, de manera que coincidan los lados de la imagen que parten de P con los lados correspondientes del soporte, que parten de P’. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, P=P’).
4.2.5. Se unen con una línea recta x mediante una regla los puntos P y E, y se prolonga dicha recta x sobre el soporte.
4.2.6. El punto de intersección en el soporte de las rectas w y x es el punto E’, que es la localización correspondiente exacta en el soporte del punto E de la imagen, que es el centro de la circunferencia.
4.2.7. Se unen con una línea recta z mediante una regla los puntos P y F, y se prolonga dicha recta z sobre el soporte.
4.2.8. El punto de intersección en el soporte de las rectas w y z es el punto F’, que es la localización correspondiente exacta en el soporte del punto F de la imagen.
4.2.9. Se traza en el soporte una circunferencia con centro en E’ y radio E’F’, mediante el método técnico que se considere más apropiado.
5. Procedimiento de reducción.
Para reducir una imagen dada se procederá siguiendo estos pasos: (Fig. 6):
Figura 6. Procedimiento de Reducción.
5.1. Se localiza el punto G de la imagen.
5.2. Se hace coincidir la esquina O’ del soporte sobre su esquina homóloga O de la imagen, de manera que coincidan los lados del soporte que parten de O’ con los lados correspondientes de la imagen, que parten de O. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, O=O’).
5.3. Se unen con una línea recta r mediante una regla los puntos G y O’, dibujando dicha recta r sobre el soporte.
5.4. Se hace coincidir la esquina P’ del soporte sobre su esquina homóloga P de la imagen, de manera que coincidan los lados del soporte que parten de P’ con los lados correspondientes de la imagen, que parten de P. (En esta ocasión el punto de coincidencia entre imagen y soporte es esa esquina, P=P’).
5.5. Se unen con una línea recta q mediante una regla los puntos G y P’, dibujando dicha recta q sobre el soporte.
5.6. El punto de intersección en el soporte de las rectas r y q es el punto G’, que es la localización correspondiente exacta en el soporte del punto G de la imagen, que es lo que se buscaba.
Además de estos pasos básicos, en el procedimiento de reducción se actuará de manera similar al resto de los pasos desarrollados más arriba, según la diferente casuística.
6. Comprobación.
Todo este método está basado en la definición de triángulos semejantes y en el Teorema primero de Tales de Mileto. Esto se constata en casos como los siguientes:
El triángulo O’P’A’ es semejante al triángulo OPA.
El triángulo O’Q’B’ es semejante al triángulo OQB.
El triángulo O’P’R’ es semejante al triángulo OPR.
El triángulo O’P’C’ es semejante al triángulo OPC. Aquí se cumple que , con lo cual se comprueba el fundamento del Teorema de Tales. Se pueden realizar comprobaciones similares en cualquiera de los casos desarrollados en el presente método.
Teniendo de referencia la figura 2 se comprueba que la diagonal O’R’ del soporte es proporcional a la diagonal OR de la imagen, con lo que soporte e imagen son proporcionales, así que el lado O’P’ del soporte es igualmente proporcional al lado OP de la imagen. Por otro lado, se mantiene la igualdad de los ángulos (el ángulo AOP es igual a su ángulo correspondiente A’O’P’, y el ángulo APO es igual a su ángulo correspondiente A’P’O’). Como consecuencia de esta igualdad de ángulos y de la proporcionalidad de lados se constata que el segmento O’A’ del soporte es proporcional al segmento OA de la imagen, y el segmento P’A’ del soporte es proporcional al segmento PA de la imagen. Así pues, se comprueba la definición de triángulos semejantes, la semejanza entre cada uno de los elementos de la imagen y del soporte y, por extensión, la semejanza íntegra entre la imagen y su representación en el soporte.
7. Formatos.
Si la imagen dada es un triángulo cualquiera y hay que ampliarla sobre un soporte igualmente triangular semejante, se actuaría de igual manera siguiendo todo el método descrito, directamente sobre el triángulo, desplazando simplemente la imagen triangular por las tres esquinas del soporte homólogo. Se procederá igualmente si se parte de cualquier otro tipo de formato (pentágono, hexágono, etcétera).
Si la imagen dada es circular y hay que ampliarla sobre un soporte igualmente circular, solamente hay que circunscribir un cuadrado a cada una de las dos circunferencias y actuar siguiendo los pasos 3.1.1. al 3.1.6. Igualmente se cumplirían los pasos 3.2.1. al 3.2.4. con respecto al perímetro de la imagen, aunque en lugar de un paralelogramo cuadrado o rectángulo se trate de una circunferencia. Con una elipse se actuaría de igual modo, inscribiéndola en un rectángulo.
Si se trata de algún tipo de superficie circular o elíptica que no permite ser inscrita en un cuadrado o un rectángulo, como podría ser una plaza circular, se actuaría trazando los diámetros perpendiculares de la circunferencia o la elipse, y utilizando los puntos de unión de esos diámetros con las curvas como puntos de coincidencia, haciendo coincidir los diámetros de la imagen y del soporte.
8. Consideraciones.
Con este método no hace falta trazar ninguna línea paralela como tal, como se menciona en el Teorema primero de Tales de Mileto, aunque lógicamente de la utilización de este método resulten rectas paralelas (así, P’A’ es paralela a PA con punto de coincidencia O=O’). Trazar rectas paralelas entre una imagen y su soporte proporcional, normalmente mucho mayor que ella, por medio de escuadra y cartabón, puede ser muy impreciso, cuando no casi imposible por la diferencia de tamaño que puede llegar a existir entre los útiles de dibujo habituales y el formato del soporte final.
Este método también funciona partiendo de cualquier otro punto de coincidencia entre imagen y soporte, como puede ser el punto medio de cada lado, pero se evitan complicaciones si se parte de los puntos más reconocibles del polígono, que son sus vértices.
Para localizar puntos situados en la mitad inferior de la imagen, se utilizará para mayor comodidad la superposición de imagen y soporte en las dos esquinas superiores, y viceversa. De igual modo, para localizar puntos situados en la mitad izquierda de la imagen, se utilizará para mayor comodidad la superposición de imagen y formato en las dos esquinas derechas, y viceversa. Como regla general, es recomendable trabajar a partir de la esquina que esté más alejada del punto que se desea trasladar, para que el margen de error al lanzar la recta sea el menor posible.
Si el soporte es demasiado grande como para utilizar reglas convencionales, siempre podrá usarse un listón rectilíneo de madera o un perfil metálico, o un cordel que puede fijarse momentáneamente mediante cualquier medio al punto que más interese y con él, bien estirado, lanzar rectas y localizar puntos distantes. De ese modo este método puede utilizarse también sobre un muro o cualquier otra superficie vertical. Igualmente puede utilizarse, con la ayuda de cordeles, sobre el suelo o cualquier otro terreno horizontal, por grande que sea. En estos casos de grandes superficies horizontales, la utilización de un método de proyección óptica resultaría muy difícil y el planteamiento de una cuadrícula sería algo muy laborioso. Por el contrario, el presente método es muy accesible tanto para casos verticales como horizontales. Es incluso más cómodo sobre una gran superficie horizontal que sobre una vertical, pues sobre la horizontal el dibujante puede desplazarse con más facilidad, y además se cuenta con la ayuda de la fuerza de la gravedad a la hora de colocar las imágenes en las esquinas y a la hora de lanzar los cordeles. A lo largo de toda la historia de la humanidad se han llevado a cabo replanteos sobre el terreno para la construcción de edificios a partir del dibujo de sus planos, a través de cordeles, estacas, plomadas, cuerdas, niveles y escuadras (Cabezas, 2008), y en este ámbito el presente método tiene mucho que aportar.
Si a la hora de realizar una ampliación el soporte no es mucho mayor que la imagen dada, de manera que esta tape casi por completo al soporte, se actuará en las franjas visibles del soporte alrededor de la imagen, en cuyos bordes siempre se podrán marcar extremos de líneas rectas, para después ir retirando la imagen y completar dichas líneas.
Si, por el contrario, se trata de realizar una reducción y el soporte no es mucho menor que la imagen dada, de manera que este tape casi por completo a la imagen, se actuará en las franjas visibles de la imagen alrededor del soporte, en cuyos bordes siempre se podrán marcar extremos de líneas rectas, para después ir super-poniendo el soporte y completar dichas líneas.
Es recomendable -aunque no imprescindible- disponer de dos imágenes idénticas que puedan fijarse a dos esquinas del soporte durante el máximo tiempo seguido posible, para aumentar la comodidad y la precisión de este método de dibujo.
Este método es mucho más limpio que el uso de cuadrícula, pues esta invade todo el soporte -o al menos buena parte de él, aunque se procure limitar la cuadrícula ajustándola a la zona donde irá el dibujo más complicado-, y puede ser muy delicado intentar eliminar la cuadrícula tras la finalización del dibujo. Por otro lado, cuanto más alta es la densidad de la cuadrícula, más puede ensuciar el soporte y si, por el contrario, la cuadrícula es poco densa, la exactitud del dibujo será escasa. Con el método aquí presentado se utilizan los puntos que cada dibujo requiera, lo cual es más limpio, y por otra parte más exacto y más rápido.
Como limitación propia de las grandes ampliaciones, cabe señalar la más obvia, derivada de la diferencia de tamaño entre la imagen dada y el soporte de ampliación, siendo conscientes de que, en la medida en que tal diferencia aumente, la precisión decaerá.
9. Conclusiones.
Para muchos dibujantes y pintores, el dibujo del natural “a mano alzada” representa una de las bases más genuinas de la plástica, a la vez que es comprensible que los artistas utilicen otros medios para agilizar su trabajo -preferiblemente una vez dominada esa base-. En estos tiempos, en los que prácticamente todo trabajo ha de pasar en algún momento por el uso de nuevas tecnologías, sistemas electrónicos y procedimientos digitales, el presente método de dibujo aporta un nuevo enfoque, directo, con un retorno a lo manual, que recupera la pura geometría clásica para aplicarla a cualquier tipo de dibujo. De hecho, este método puede ser de interés en ámbitos tan variados como el urbanismo, la jardinería, la ingeniería, la publicidad, el teatro, la agricultura o el deporte. En el campo puramente plástico, este método de dibujo puede aplicarse en la pintura de caballete, en el dibujo de taller, en la pintura mural y en el grafiti, y puede ser de utilidad para todo aquel que esté interesado, por profesión, aprendizaje o curiosidad, en las técnicas de escalado proporcional de la imagen.
Bibliografía
Barbero et al. (2002). Máquinas y herramientas de dibujo. Madrid, España: Cátedra.
Cabezas, L. (2008). El dibujo como invención. Madrid, España: Cátedra.
Ceac (Ed.). (2002). Dibujo y Pintura. Técnicas y Materiales. La perspectiva. Barcelona, España: Ceac.
Da Vinci, L. (2010). Tratado de pintura. Madrid, España: Akal.
Euclides. (1994). Elementos (Libros 5º-9º). Madrid, España: Gredos.
Lawson, P. (1958). Perspectiva para dibujantes. Barcelona, España: Gustavo Gili.
Maveco (Ed.). (1987). Enciclopedia Didáctica de Dibujo y Pintura (Tomo 1). Madrid, España:
Maveco.
Szunyoghy, A. (2013). El dibujo del retrato. Potsdam, Alemania: Ullmann.
Ulrich, G. (1974). El mundo de la pintura. Barcelona, España: Círculo de Lectores.
Ubach, T. (Ed.). (2008). El arte del dibujo. Barcelona, España: Parramón.





No hay comentarios:
Publicar un comentario